 | |
МЕНЮ
- Главная
- Астрономия и космонавтика
- Банковское биржевое дело и страхование
- Биология и естествознание
- Бухгалтерский учет и аудит
- Авиация и космонавтика
- Административное право
- Арбитражный процесс
- Архитектура
- Астрология
- Астрономия
- Банковское дело
- Безопасность жизнедеятельности
- Журналистика
- Зоология
- Инвестиции
- История
- Кибернетика
- Коммуникации и связь
- Кулинария
- Культурология
- Логика
- Логистика
- Маркетинг
- Фотография
- Химия
- Хозяйственное право
- Цифровые устройства
- Экологическое право
- Экология
- Экономика
- Карта сайта
Курсовая: Системы стабилизации и ориентации
Курсовая: Системы стабилизации и ориентации
Реферат
В данном курсовом проекте изучаются методы анализа и синтеза систем
стабилизации и возможность применения для этого математического пакета MAPLE
V. Разработана библиотека процедур, позволяющая облегчить работу студентов
при выполнении курсового проекта по дисциплине «Системы стабилизации и
ориентации».
Пояснительная записка содержит 36 листов, 3 приложения и 7 рисунков.
Содержание
Введение
1 Обзор литературы
1.1
Получение дискретной модели непрерывной системы...
1.2
Передаточные функции непрерывных и дискретных
систем.......................
1.3 Частотные характеристики
непрерывных и
дискретных
систем..............................................................
1.4 Анализ устойчивости непрерывных и
дискретных
систем.......................................................
1.5
Синтез цифровых систем управления по желаемым
частотным
характеристикам разомкнутой системы.........
2 Разработка
библиотеки процедур в среде Maple 2.1 Получение
дискретной модели непрерывной системы........
2.1.1
Процедура diskretA........................................................
2.1.2 Процедура
diskretB........................................................
2.2 Получение матрицы передаточных функций......
2.2.1 Процедура
permatr.........................................................
2.3 Построение частотных характеристик дискретной и
непрерывной систем.................
2.3.1 Процедура
afch................................................................
2.3.2 Процедура
lach................................................................
2.3.3 Процедура
lfch................................................................
2.4 Анализ устойчивости дискретной и непрерывной систем
2.4.1 Процедура
klark..............................................................
2.4.2 Процедура
gurvitz...........................................................
2.4.3 Процедура
ust..................................................................
2.5 Синтез дискретных систем
2.5.1 Процедура
sintez1...........................................................
2.5.2 Процедура
sintez2...........................................................
3 Апробация библиотеки процедур SSO.....................................
Заключение...................................................................
...................
Список
литературы...................................................................
......
Введение
В настоящее время в промышленности и сельском хозяйстве применяются десятки
тысяч систем автоматического регулирования (САР), которые обеспечивают
высокую эффективность производственных процессов. Поэтому теория
автоматического регулирования изучается во всех высших учебных заведениях в
качестве одной из базовых дисциплин. На её основе в дальнейшем читаются
такие курсы, как теория автоматического управления, автоматизированные
системы переработки информации, управление технологическими и организационно-
экономическими процессами, теория автоматизированного проектирования систем и
их математическое обеспечение, а также целый ряд дисциплин специального
назначения. Объекты и устройства систем регулирования отличаются по своей
физической природе и принципам построения, поэтому проектировщику необходимо
не только иметь хорошую подготовку в области механики, электроники,
электротехники и вычислительной техники, но и уметь учитывать специфические
особенности объекта. С целью овладения практическими навыками использования
методов теории автоматического регулирования будущие специалисты в процессе
обучения выполняют домашние задания, курсовые и дипломные работы по
проектированию систем управления конкретными объектами.
Трудность выполнения проектных работ в значительной степени определяется
сложностью математического аппарата, используемого при описании объектов и
систем автоматического регулирования. Поэтому для облегчения решения задач
теории автоматического регулирования имеет смысл создание процедур,
реализующих ряд алгоритмов проектирования систем. Они позволяют формировать
обобщенные модели элементов в дискретной форме и матрицы передаточных
функций; строить амплитудно-фазовые частотные характеристики (в обычном и
логарифмическом масштабах) и др.
1 Обзор литературы
1.1 Получение дискретной модели непрерывной системы
При проектировании непрерывных, дискретно-непрерывных и дискретных САР
необходимо располагать математической моделью элемента (объекта). При высоких
порядках моделей удобно пользоваться уравнениями, составленными во временной
области и записанными в векторно-матричной форме. Рассмотрим одну из наиболее
часто встречающихся форм представления многоконтурных стационарных линейных
элементов (объектов). При этом будем считать, что в линейный объект
регулирования после ряда преобразований входят лишь две матрицы: А и
В. Тогда эту форму представления стационарного объекта можно записать в виде
векторно-матричного уравнения
![]() , (1.1)
, (1.1)
где у и u - векторы размерностей (n ´ 1) и (m
´ 1); А и В - матрицы размерности (n´ n) и (n´
m).
С целью использования одинаковой формы описания объектов непрерывных,
дискретно-непрерывных и дискретных САР пользуются теорией спектрального
разложения матриц, которая с помощью специально созданных алгоритмов
позволяет получать единые математические модели в дискретной форме. К
основному преимуществу такого подхода следует отнести возможность
представления моделей с использованием матриц до 50-80-го порядков, без
существенного понижения точности спектрального разложения матриц.
Рассмотрим алгоритмы, с помощью которых составляются дискретные модели
многомерных объектов, описываемых типовым векторно-матричным уравнением (1.1).
Аналитическое решение этого уравнения при начальных условиях y(t0
) имеет вид
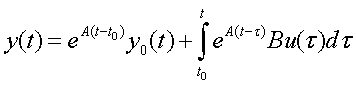 (1.2)
(1.2)
В моменты времени t=кT0 и t=(к+1)Т0
состояние объекта ук+1 связано с предыдущим состоянием у
к соотношением
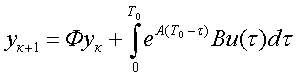 (1.3)
(1.3)
где ![]() - переходная матрица системы уравнений.
- переходная матрица системы уравнений.
Математические зависимости для алгоритмов дискретных моделей можно составить
с тремя типами экстраполяторов.
Самая простая дискретная модель может быть получена, если положить, что внутри
интервала квантования сигнала, и (t) экстраполируется по
одной точкеступеньки со значениями ик , т.е. перед
объектом включен экстраполятор нулевого порядка Э0. В этом
случае соотношение (1.3) можно представить в виде
ук+1=Фук+Fик . (1.4)
Здесь F=(Ф - I)А-1В - матрица коэффициентов, обеспечивающих передачу
сигналов по входам дискретной модели.
1.2 Передаточные функции непрерывных и дискретных систем
Под передаточной функцией стационарных элементов понимают отношение
изображения выходной величины к изображению функции входной величины,
полученные при нулевых начальных условиях. Для многоконтурных стационарных
элементов возможно получение матрицы передаточных функций на основе модели
системы во временной области в векторно-матричной форме (1.1). Применяя
преобразование Лапласа, получим:
IX(s)=AX(s)+BU(s), (1.5)
где I - единичная матрица. Путем несложных преобразований найдем:
X(s)=(Is – A)-1BU(s). (1.6)
Таким образом, матрицу передаточных функций в общем виде можно записать так:
MU=X(s)/U(s)=(Is – A)-1B (1.7)
1.3 Частотные характеристики непрерывных и
дискретных систем
Частотные характеристики линейных непрерывных систем находятся из передаточных
функций после подстановки в них s=jw и выделения действительной мнимой
частей, т.е.
W0(jw)=U0(w)+jV0(w), (1.8)
где U0(w) и V0(w) - соответственно
действительная и мнимая частотные характеристики.
Пользуясь выражением (1.8), в декартовой системе координат строят
амплитудно-фазовые частотные характеристики W0(jw). Если
перейти к полярной системе координат, то выражение (1.8) можно переписать в
виде
![]() (1.9)
(1.9)
где ![]() и q0(w) - соответственно амплитудная и фазовая частотные характеристики.
и q0(w) - соответственно амплитудная и фазовая частотные характеристики.
Из выражений (1.8) и (1.9) можно найти формулы для вычисления амплитудной и
фазовой частотных характеристик:
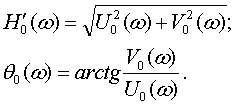 (1.10)
(1.10)
Частотные характеристики линейных дискретных систем находятся путем подстановки
в передаточные функции ![]()
.
На практике амплитудные и фазовые частотные характеристики строят на
полулогарифмической бумаге. Тогда ось w размечают в логарифмическом масштабе,
где изменение частоты в 10 раз называется декадой, амплитуду ![]()
откладывают в децибелах и фазу q в градусах.
1.4 Анализ устойчивости непрерывных и дискретных систем
Системы стабилизации должны обеспечивать устойчивость и заданную точность
регулирования отклонений углов и координат центра масс ЛА от программных
значений. При этом могут налагаться ограничения на значения отдельных
параметров системы (управляющие воздействия или производные управляющих
воздействий). Отклонения углов и угловых скоростей могут ограничиваться для
определенных возмущающих воздействий.
Задача обеспечения устойчивости является доминирующей при синтезе систем
стабилизации ЛА. Движение системы на конечном интервале времени считается
устойчивым, если на этом интервале при заданных начальных условиях и
действующих возмущений его параметры не превышают заданных ограничений -
техническая устойчивость. Если система содержит существенные нелинейности, то
для устойчивости при заданных начальных условиях и действующих возмущений
необходимо чтобы при начальной амплитуде периодической составляющей,
превышающей её установившееся значение с течением времени эта амплитуда
стремилась к своему установившемуся значению, а параметры установившегося
движения не превышали заданных ограничений.
Для анализа устойчивости линейной или линеаризованной системы используется
понятие асимптотической устойчивости, при этом обычно Используется
стационарные математические модели, полученные с использованием метода
замороженных коэффициентов. Система является асимптотически устойчивой, если:
·для непрерывных систем - корни характеристического полинома лежат в левой
полуплоскости;
·для дискретных систем - корни характеристического полинома лежат внутри
окружности единичного радиуса.
Устойчивость непрерывных систем может исследоваться с помощью первого метода
Ляпунова, а также алгебраических критериев (Гурвица, Рауса и Льенара-Шепара).
Для дискретных систем используется критерий Кларка и Шур-Кона. Основным
недостатком применения данных критериев следует считать невозможность
получения при этом оценок качества и точности. Пользуясь ими для систем
высокой размерности, проектировщик не может дать рекомендаций по выбору
параметров, не только обеспечивающих запасы устойчивости, но и
удовлетворяющих требованиям к качеству и точности процессов регулирования.
Следует отметить, что на устойчивость дискретных нелинейных систем большое
влияние оказывает выбор такта квантования.
Частотные критерии устойчивости предполагают использование передаточных функций
для описания системы регулирования и справедливы при её полной наблюдаемости и
управляемости. Тогда критерий устойчивости по Ляпунову аналогичен критериям
Михайлова, Михайлова-Найквиста и D-разбиениям Неймарка. Эти критерии применимы
к анализу как непрерывных, так и дискретных систем. Однако в первом случае они
базируются на методах s-преобразований, во втором - z-преобразований. Положив
s=jw или z=ejwT0, строятся
частотные характеристики, по которым определяются устойчивости систем
регулирования по фазам и модулям и с помощью специальных номограмм оценивают
показатели качества и характеристики точности. Большим преимуществом частотных
критериев устойчивости является возможность их распространение и на многие типы
нелинейных систем.
При проектировании систем стабилизации ЛА чаще всего используются
алгебраические и частотные критерии, реже корневые.
1.4.1 Корневые критерии заключаются в вычислении корней
характеристического полинома замкнутой системы.
1.4.2 Алгебраические критерии устойчивости не требуют выполнения
вычислительной процедуры определения корней характеристического уравнения и
при относительно невысоких порядках дифференциальных уравнений (до 15-го)
позволяют находить условия устойчивости автономных замкнутых систем.
А(s)=ansn + an-1sn-1+ an-2
sn-2+.+a0. (1.11)
Критерий Гурвица. Корни характеристического уравнения (1.11) n-го порядка
будут иметь отрицательные действительные части, если составленный из его
коэффициентов аi> 0 определитель
 (1.12)
(1.12)
и все его диагональные миноры
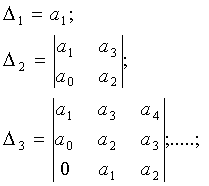 (1.13)
(1.13)
положительны.
Критерий Рауса. Зная коэффициенты характеристического уравнения,
составляют таблицу Рауса(табл. 1.1). Для того чтобы замкнутая система была
устойчива асимптотически, необходимо и достаточно, чтобы все коэффициенты Рауса
первого столбца таблицы при аi>0 были положительны, т.е. сi
,1>0 (i=1,2,.). Для вычисления элементов табл. 1.1 можно использовать
следующие рекуррентные формулы:
для первой строки таблицы
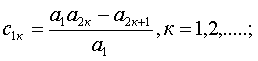 (1.14)
(1.14)
для второй строки таблицы
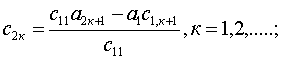
![]() (1.15)
(1.15)
для остальных строк
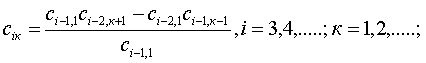
(1.16)
Таблица 1.1
| Номера строк | Номера столбцов | ||||
| 1 | 2 | 3 | ... | I | |
| Коэффициенты с четными индексами | |||||
а0 | а2 | а4 | ... | ||
| Коэффициенты с нечетными индексами | |||||
а1 | а3 | а5 | .... | ||
| 1 | С11 | С12 | С13 | .... | С1i |
| 2 | С21 | С22 | С23 | .... | C2i |
| .. | .. | ... | ... | ... | .. |
| к | Ск1 | Ск2 | Ск3 | .... | Сiк |
Критерий Шур-Кона. Данный критерий позволяет анализировать устойчивость
дискретных и дискретно-непрерывных систем по характеристическому полиному
замкнутой системы, записанному в форме z-преобразования. Для уравнения n-го
порядка имеем
A(z)=anzn+ an-1zn-1+ an-2
zn-2+.+a0.
(1.17)
По уравнению запишем коэффициенты в виде определителя
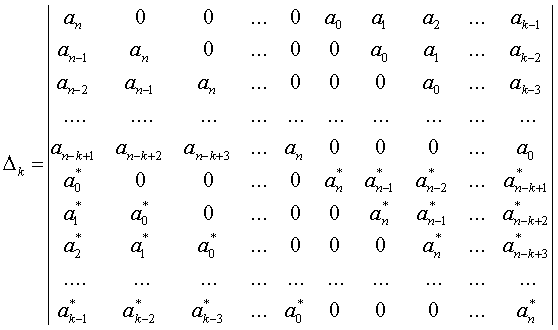
(1.18)
где k=1,2,.,n; a*- сопряженные значения тех же коэффициентов.
Корни характеристического уравнения (1.18) будут находиться внутри единичной
окружности, если коэффициенты уравнения (1.17) удовлетворяют всем определителям
Шур-Кона, имеющего Dk < 0 - для нечетных k и Dk >
0 для четных k. В этом случае система будет устойчива
Критерий Кларка. Представляет собой совокупность 3-х необходимых условий,
Страницы: 1, 2
ИНТЕРЕСНОЕ
© 2009 Все права защищены. |